Context

I'm working on generating random landscapes (just a fun project), this obviously needs a lot of random numbers, also it needs random distributions.

For example the basic land generation algorithm I use is as follows:

1. Start with empty matrix;
2. Add to the matrix gaussian multivariate distribution, with mean taken randomly from range (0, 1) and standard deviation on X axis equal to taken from (.1, 1) and on y from (1, 5).
3. If finished exit;
4. GOTO 1;

Example landscape generated by the algorithm. Brighter dots mean higher.

The problem is that the above will give me distributions that are parallel to the X or Y axes (or in precise terms --- they will give me distributions of uncorrelated variables).

To introduce skew you'll need to provide full covariance matrix.

The problem is that you can't just provide arbitrary matrix as covariance, as covariance matrix needs to be "positive semi-definite" (what this property means is not really important). This is not a problem if you make one or two, covariance matrices by hand, but I need to generate thousands of them.

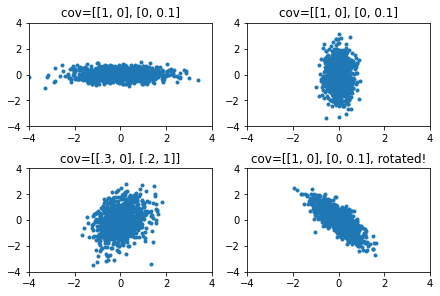
Examples of distributions with different covariances.

I tried googling for a solution for this problem, and to no avail, found no algorithm on how to create arbitrary covariance matrix.

How to generate arbitrary (and explainable) multivariate gauss distributions

To generate points from multivariate gauss distributions you need three parameters:

• standard deviation and mean on X axis;
• standard deviation and mean on Y axis;
• angle between the distribution and X axis;

Algorithm is then as follows:

1. Generate point from distribution of X an Y mean equal to zero;
2. Rotate the point by angle theta;
3. Add X and Y means to the point;

In other worlds:

rotate_matrix = np.array(
    [[np.cos(theta), -np.sin(theta)], [np.sin(theta), np.cos(theta)]]
)
rand = numpy.random.RandomState(12)
result = np.zeros(2, dtype=float)
result[0] = rand.normal(0, self.stddev[0])
result[1] = rand.normal(0, self.stddev[1])

if self.rotate_radians is not None:
    result = np.dot(rotate_matrix, result)

result[0] += self.mean[0]
result[1] += self.mean[1]

If you want to have not points belonging to the distribution, but probability density function, then this recipe won't help you.

In my random landscape generator I need both of the above, so for probability density function there are two solutions:

1. To the same rotation trick, but on distributions, however now rotation trick is now harder --- as you need to use "rotate image" functions that use interpolation.

2. Select elements that represents correlation randomly, and if covariance matrix is not positive semidefinete, just re-try.

   Here is the example code:

   for attempt in range(attempts):
       covariance[0][1] = random_gen.uniform(-abs(covariance[1][1]), +abs(covariance[1][1]))
       covariance[1][0] = random_gen.uniform(-abs(covariance[0][0]), +abs(covariance[0][0]))
       try:
           return make_hill(context.point_positions, mean, covariance, height)
       except ValueError as e:
           if attempt == attempts - 1 and raise_on_error:
               raise ValueError(mean, stddev, height) from e